[Algorithm] Dynamic Programming (DP)

Dynamic Programming (DP)

• 여러개의 하위문제(Subproblem)를 통해 문제를 해결하는 알고리즘
• ‘동적계획법’ 이라고 불린다.
• Dynamic 에 특별한 의미는 없다.

Example

Fibonacci numbers

[0, 1, 1, 2, 3, 5, 8, 13, 21 . . .]

• F₀ = 0

• F₁ = 1

• F_n = F_n-1 + F_n-2 (n >= 2)

Python Implementation Code

def fibo(n):
    if n == 0:
        return 0
    elif n == 1:
        return 1
    return fibo(n-1) + fibo(n-2)

현재 코드는 중복 호출이 많아 비효율적이다.
이 문제를 해결하는 방법은 아래의 Approach 항목에서 다룬다.

Property

Overlapping Subproblem

• 문제가 여러번 반복되는 하위문제로 나누어진다.

• 하위문제 또한 반복되는 하위문제로 나누어지며 이를 통해 해를 구할 수 있다.
  (새로운 하위문제를 생성하지 않는다.)

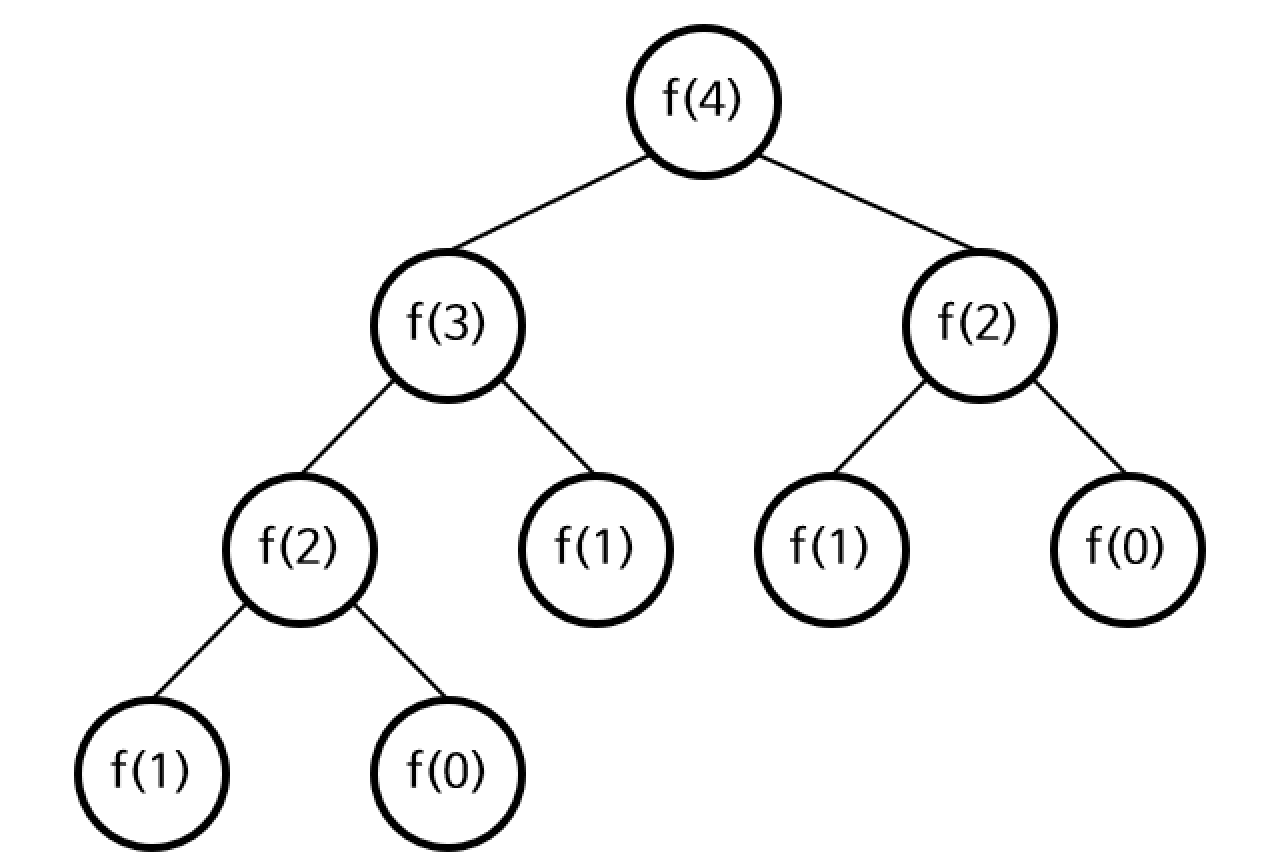
위의 이미지는 fibo(4) 를 실행했을 경우
재귀 호출되는 것을 이미지화한 것이다.
중복되는 함수호출을 표시해보면 아래와 같다.

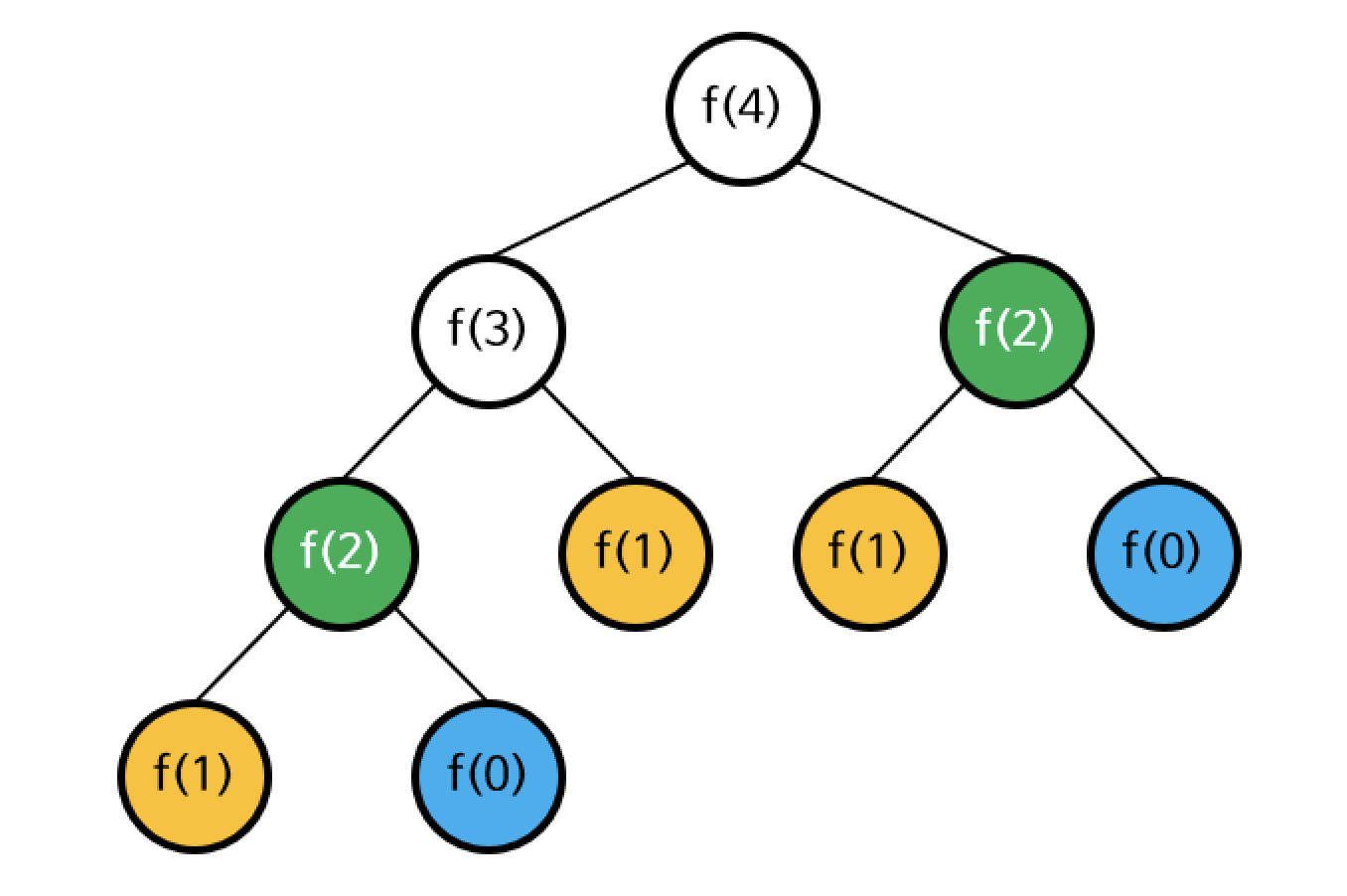
이를 통해 피보나치 수열은 반복되는 하위문제로 나누어짐을 알 수 있다.

Optimal Substructure

• 하위문제의 최적해로 문제의 최적해를 구할 수 있다.

• ex) 피보나치의 수열: F_n = F_n-1 + F_n-2 (n >= 2)

Approach

Memoization (Top-Down)

중복되는 함수 호출을 방지하기 위해
임의의 메모리에 해당 값들을 저장한 뒤 필요할 때 호출하는 방식

Property

• 일반적으로 재귀를 사용한다.

• 많은 재귀 호출로 인해 상대적으로 속도가 느리다.

• 상대적으로 코드가 간결하다.

Python Implementation Code

Use dict

d = {0:0, 1:1}  # Define tmp dict for Memoization
def fibo(num):
    if num not in d.keys():
        d[num] = fibo(num-1) + fibo(num-2)  # Memoization
    return d[num]

Tabulation (Bottom-Up)

최하위 문제의 해부터 순차적으로 구하여 최종 문제의 해를 구하는 방법

Property

• 일반적으로 반복문을 사용한다.

• 많은 조건이 주어질 경우 상대적으로 코드가 복잡해진다.

Python Implementation Code

Use list

# 1

def fibo(n):
    d = [0, 1]
    for i in range(2, n+1):
        d.append(d[i-1] + d[i-2])
    return d[n]

# 2

def fibo(num):
    d = [0] * (num+1) if num > 0 else [0, 0]
    d[0] = 0
    d[1] = 1
    for i in range(2, num+1):
        d[i] = d[i-1] + d[i-2]
    return d[num]

Use dict

def fibo(n):
    d = {0:0, 1:1}
    for i in range(2, n+1):
        d[i] = d[i-1] + d[i-2]
    return d[n]