[Data Structure] Adjacency Matrix & Adjacency List

Objective

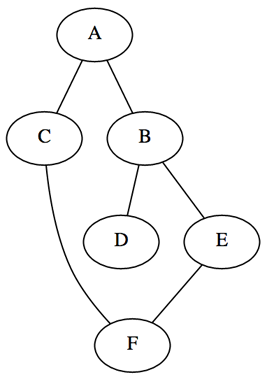
그래프 관련 문제를 풀 때는, 문제 상황을 그래프로 모델링한 후에 푸는 것이 보편적이다.
위와 같은 그래프가 있다고 가정하자. 노드 A에서 시작하여 그래프의 모든 노드를 방문하려면 어떻게 해야할까?
먼저, 그래프의 노드 간 연결관계를 나타내야 할 것이다. 표현 방법으로는 크게 Adjacency matrix(인접 행렬)과 Adjacency list(인접 리스트)가 있다.

Adjacency Matrix

접 행렬은 그래프의 연결 관계를 이차원 배열로 나타내는 방식이다. 인접 행렬을 ad[][]라고 한다면 adg[i][j]에 대해서 다음과 같이 정의할 수 있다.

adj]i][j] : 노드 i에서 노드 j로 가는 간선이 있으면 1, 아니면 0
cf.) 만약 간선에 가중치가 있는 그래프라면 1 대신에 가중치의 값을 직접 넣어주는 방식으로 구현

Python Implementation Code

             # A, B, C, D, E, F
adj_matrix = [[0, 1, 1, 0, 0, 0],  # A
              [1, 0, 0, 1, 1, 0],  # B
              [1, 0, 0, 0, 0, 1],  # C
              [0, 1, 0, 0, 0, 0],  # D
              [0, 1, 0, 0, 0, 1],  # E
              [0, 0, 1, 0, 1, 0]]  # F

Characteristic

위의 그래프처럼 무향그래프에서는 노드 i에서 노드 j로 가는 간선이 있다는 말은 노드 j에서 노드 i로 가는 간선도 존재한다는 말이 된다.
따라서, 인접 행렬이 대각성분(adj[i][j]에서 i=j인 원소들)을 기준으로 대칭인 성질을 가지게 된다. 위와 같은 무향 그래프가 아닌 유향 그래프라고 하면 인접 행렬은 비대칭이 된다.

Pros

인접 행렬의 장점은 구현이 쉽다는 점 이다.
그리고, 노드 i와 노드 j가 연결되어 있는지 확인하고 싶을 때, adj[i][j]가 1인지 0인지만 확인하면 되기 때문에 O(1)이라는 시간 복잡도에 확인할 수 있는 점 도 있다.

Cons

하지만, 전체 노드의 개수를 |V|개 간선의 개수를 |E|개라고 해보자. 노드 i에 연결된 모든 노드들에 방문해 보고 싶은 경우 adj[i][1]부터 adj[i][j]를 모두 확인해 보아야 하기 때문에 총 O(|V|)의 시간이 걸린다. 따라서 모든 노드에 대해 다른 노드들을 방문하기 위해서는 O(|V|^2)만큼의 시간이 걸린다.
위의 그래프와 같은 경우 큰 차이가 느껴지지 않을 수도 있지만, 노드의 개수에 비해 간선의 개수가 훨씬 적은 그래프라면 이야기가 달라질 것이다. 만약, 노드의 개수는 총 1억개인데 각 노드마다 연결된 간선이 많아봤자 2개인 그래프가 있다고 가정해보자. 그렇다면, 특정 노드와 연결된 노드들이 몇 번 노드인지 확인하기 위해 총 1억 개의 노드들을 모두 확인해봐야 하는 치명적인 문제가 발생하게 된다. 정작 연결된 노드는 많아봤자 2개 뿐인데 말이다.

Adjacency list

이러한 인접행렬의 단점을 보완할 수 있는 연결 관계 방식이 인접 리스트이다. 인접 리스트는 그래프의 연결 관계를 dictionary{node name: adj[]}로 나타내는 방식이다. 이 때, node name은 노드의 번호나 이름을 직접 저장하고, adj[]는 인접리스트로 다음과 같이 정의할 수 있다. > adj[i] :노드 i에 연결된 노드들을 원소로 갖는 리스트
cf) 만약 간선에 가중치가 있다면 tuple을 이용하여 tuple의 first에는 노드의 번호나 이름, second에는 간선의 가중치를 저장하는 방식으로 구현

Python Implementation Code

adj_list = {'A': set(['B', 'C']),
            'B': set(['A', 'D', 'E']),
            'C': set(['A', 'F']),
            'D': set(['B']),
            'E': set(['B', 'F']),
            'F': set(['C', 'E'])}

Pros

인접 리스트는 인접 행렬과 달리, 실제로 연결된 노드들에 대한 정보만 저장하기 때문에, 모든 벡터들의 원소의 개수의 합이 간선의 개수와 같다는 점이 있다. 즉, 간선의 개수에 비례하는 메모리만 차지 한다고 볼 수 있다.
인접 리스트의 경우에는 각 노드마다 연결된 노드만 확인하는 것이 가능하기 때문에, 전체 간선의 개수만큼만 확인해 볼 수가 있다. 따라서, O(|V|+|E|)의 시간 복잡도를 가진다고 할 수 있다. 이렇게 각 노드에 연결된 모든 노드를 방문해 보아야 하는 경우, 인접 리스트로 연결 관계를 저장하는 것이 시간상 큰 이점 을 가진다.

Cons

하지만, 인접 리스트에도 치명적인 단점이 존재한다. 노드 i와 노드 j가 연결되어 있는지 알고 싶다면 adj[i]가 참조하는 리스트 전체를 돌며 j를 성분으로 갖는지 확인 해 보아야 하기 때문이다. 따라서 시간 복잡도는 O(|V|)가 된다. 위에서 언급했듯이, 인접 행렬의 경우 adj[i][j]가 1인지 0인지만 확인하면 되기 때문에 O(1)의 시간 복잡도를 갖게 되지만 말이다.

Conclusion

그래프 문제에서 문제의 상황에 따라 인접 행렬이나 인접 리스트를 이용해서 연결 관계를 저장하여 활용하는 것이 중요하겠다.

Reference

• http://ejklike.github.io/2018/01/05/bfs-and-dfs.html
• https://sarah950716.tistory.com/12#footnote_link_12_1
• http://eddmann.com/posts/depth-first-search-and-breadth-first-search-in-python/
• McDowell, G. L. (2016). Cracking the Coding Interview: 189 Programming Questions and Solutions. CareerCup, LLC.
• http://blog.eairship.kr/269